从三道逻辑分析题看GPT4

1
2
3
4
5
6

三个逻辑学家下班后想在一起喝一杯，就来到一家酒吧。服务员问：给你们所有人都来杯酒？
第一个说，我不知道。
第二个说，我也不知道。
第三个说：是的。

为什么第三人说“是的”。

1

第三个逻辑学家的回答是“是的”，是因为如果服务员给所有人都倒一杯酒，那么第三个逻辑学家也会被包括在内。这里是一种间接的否定方式，他的意思是“不会有任何一个人不能喝酒，所以给所有人都来一杯酒”。

1
2
3
4
5
6
7
8
9

这个问题涉及到了逻辑推理。在这个场景中，三个逻辑学家下班后想喝酒。当服务员询问他们是否所有人都需要酒时，他们的回答反映了他们的观察和思考。我们可以分析每个逻辑学家的回答：

1. 第一个逻辑学家说：“我不知道。” 这表明他自己想喝酒，但不知道其他两人是否想喝。如果他自己不想喝，他会直接回答“不是”。

2. 第二个逻辑学家听到了第一个的回答，所以知道第一个逻辑学家想喝酒。然后他说：“我也不知道。” 这表示他自己也想喝酒，但仍然不知道第三个人是否想喝。如果第二个逻辑学家不想喝酒，他会知道答案是“不是”。

3. 第三个逻辑学家听到了前两个人的回答，所以知道第一个和第二个逻辑学家都想喝酒。然后他说：“是的。” 这表明他也想喝酒。因为前两个人都想喝酒，他可以确信所有人都想喝酒，所以回答“是的”。

通过逻辑学家们的回答，他们能够推理出彼此是否想喝酒，最终得出所有人都想喝酒的结论。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

这个逻辑笑话的关键在于逻辑学家们的回答方式和推理过程。让我们一步一步分析：

1. **服务员的问题**：给你们所有人都来杯酒吗？
2. **第一个逻辑学家的回答**：我不知道。
   - 这意味着第一个逻辑学家自己想要一杯酒，但不能确定其他两个人是否也想要。
3. **第二个逻辑学家的回答**：我也不知道。
   - 这意味着第二个逻辑学家知道第一个逻辑学家想要酒（因为如果第一个不想要酒，他会直接说“不”），但是他自己也想要酒，并且他还不确定第三个人是否想要。
4. **第三个逻辑学家的回答**：是的。
   - 既然第三个逻辑学家听到了前两个逻辑学家的回答，他知道前两个都想要酒。如果他自己也想要酒，那么所有人都想要酒，所以他可以确定地回答“是的”。

因此，第三个逻辑学家通过前两个逻辑学家的不确定性推理出他们都想要酒，再结合自己的意愿，最终得出所有人都想要酒的结论。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

这个问题有一个简单的推理解答:

1) 第一个人说"我不知道",说明他不知道另外两个人的答案。

2) 第二个人也说"我不知道",说明他也不知道前一个人和后一个人的答案。

3) 只有第三个人说"是的",这表明他知道前两个人的答案。

为什么他会知道?因为作为逻辑学家,他们都知道:如果任何一个人说"是的",那服务员就会给他们三个人都来杯酒。

而第三个人知道前两个人都说"不知道",所以他才会肯定地说"是的",以确保服务员给他们三个人都上酒。

总的来说,第三个人说"是的"是因为他知道前面两个人的答案,并根据逻辑推断了整个情况。

1
2
3
4
5
6
7
8
9

三个逻辑学家进入酒吧,服务员问他们是否都要一杯酒。

第一个逻辑学家说“我不知道”,表示他自己是否要酒取决于其他两个人的选择。

第二个同样表示自己不知道,也就是说自己是否要酒取决于第三个人的选择。

那么当第三个人说“是的”时,他就代表了所有三个人要酒,因为前两个人都表示要根据第三个人来决定。

第三个逻辑学家说“是的”,表示他们三个人都要来一杯酒。因为第一个逻辑学家表示要看第二个的态度,第二个要看第三个的态度,所以第三个逻辑学家的选择就代表了所有三个人的选择。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

这个谜题利用了逻辑学家的推理能力和语义上的巧妙表达。

原因是第三个逻辑学家根据前两个人的回答"我不知道",推断出了一个有趣的结论。

第一个人说"我不知道",可能有两种解释:
a) 他真的不知道自己是否要酒
b) 他知道自己要酒,但装作不知道

第二个人说"我也不知道",就暗示了他观察到第一个人的回答是"不知道"。
a) 如果第一个人真的不知道自己要不要酒,第二个人的"不知道"也可能是真实的
b) 但如果第一个人是在装作不知道,那么第二个人的"不知道"就是虚假的

第三个人意识到,如果前两个人都真的不知道自己要不要酒,那他就无法下定论。但是如果有一个人是在装作不知道,那就意味着另外两个人肯定都要酒。

所以当第三个人说"是的",表示他推断出前两个人至少有一个人是在装作不知道,因此所有人都要酒。这正是利用了逻辑和语义上的巧妙逻辑推理。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

这是一个很有趣的逻辑推理问题。让我们一步步分析为什么第三个逻辑学家能够确定地说"是的"：

1. 问题的关键在于服务员的问题："给你们所有人都来杯酒？"

2. 每个逻辑学家只知道自己是否想喝酒，但不知道其他人的意愿。

3. 第一个逻辑学家说"我不知道"，这意味着：
   - 他自己是想喝酒的（否则他会直接说"不"）
   - 但他不确定其他两人是否都想喝

4. 第二个逻辑学家说"我也不知道"，这意味着：
   - 他也是想喝酒的（否则他会说"不"）
   - 但他不确定第三个人是否想喝

5. 当轮到第三个逻辑学家时，他可以推断：
   - 前两个人都想喝酒（否则他们会直接说"不"）
   - 现在只取决于他自己是否想喝

6. 因为第三个逻辑学家说"是的"，这意味着他也想喝酒。

所以，第三个逻辑学家能够确定地说"是的"，因为他通过前两个人的回答推断出他们都想喝酒，而他自己也想喝。因此，他可以肯定地回答服务员的问题：是的，所有人都想喝酒。

这个问题展示了如何通过逻辑推理从有限的信息中得出结论，这正是逻辑学家们所擅长的。

1

下面是一个戴帽子的游戏，现在有2 顶黑帽子，3 顶白帽子，主持人用黑布蒙上A、B、C三人的眼睛，并在每个人头上戴一顶帽子，剩下的两顶藏起来，然后解开B、C的蒙眼布，让他们三个人分别说出自己头上戴的帽子颜色，B、C看着别人头上的帽子却都回答不上来。这个时候A却说他知道了 ，她戴的是白色。主持人说对，请问 A是怎么推理的

1

A可以推断出自己戴的是白色帽子，因为如果B或C看到自己和另一个人都戴黑帽子，那么他们就可以推断自己戴白帽子，但是他们都无法回答，说明两者中至少有一个人戴白帽子，那么A就知道自己戴白帽子了。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18

A 知道有 2 顶黑帽子和 3 顶白帽子。当 B 和 C 的蒙眼布被解开时，A 仍无法看到其他人头上的帽子颜色，但可以听到 B 和 C 的回答。

首先，B 看到了 C 的帽子，有以下两种可能：

1. 如果 C 戴着黑帽子，那么 B 知道还有 1 顶黑帽子和 3 顶白帽子。此时，B 知道自己戴的帽子颜色可能是黑色（剩下的一顶黑帽子）或白色（3 顶白帽子中的一顶）。
2. 如果 C 戴着白帽子，那么 B 知道有 2 顶黑帽子和 2 顶白帽子。此时，B 知道自己戴的帽子颜色可能是黑色（2 顶黑帽子中的一顶）或白色（2 顶白帽子中的一顶）。

由于 B 无法确定自己戴的帽子颜色，接下来轮到 C 推理。此时，C 已知 B 看到了 C 戴的帽子颜色，但无法确定 B 戴的帽子颜色。因此，C 可以推测如下：

1. 如果 B 看到了 C 戴的是黑帽子，那么 C 知道 B 有可能看到剩下的一顶黑帽子和 3 顶白帽子。此时，C 会认为自己戴的帽子颜色可能是黑色或白色。
2. 如果 B 看到了 C 戴的是白帽子，那么 C 知道 B 看到有 2 顶黑帽子和 2 顶白帽子。此时，C 怀疑自己戴的帽子颜色可能是黑色（2 顶黑帽子中的一顶）或白色（2 顶白帽子中的一顶）。

因为 C 也无法确定自己戴的帽子颜色，A 可以从 B 和 C 的回答中得出一些信息。A 可以推理如下：

1. 如果 B 和 C 都看到了对方戴的是黑帽子，那么他们应该能够确定自己戴的是白帽子（因为只有 2 顶黑帽子）。
2. 但实际上，B 和 C 都无法判断自己戴的帽子颜色。这意味着他们看到的是对方戴的白帽子，因为如果他们看到的是黑帽子，他们会知道自己戴的是白帽子。

所以，A 可以推理出自己戴的是白帽子，因为 B 和 C 都无法确定自己戴的帽子颜色。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22

这是一个经典的逻辑推理问题，涉及到三人戴帽子的情境。让我们一步步分析A是如何推理出自己戴的是白帽子。

1. **帽子数量**：有2顶黑帽子和3顶白帽子。

2. **B和C的观察结果**：
    - B和C都看到了A和对方头上的帽子，但都无法确定自己帽子的颜色。

3. **B的推理**：
    - 假设如果A和C都戴着黑帽子，那么B就会立刻知道自己戴的是白帽子（因为只剩两顶黑帽子）。
    - 但B回答不上来，说明A和C中至少有一人戴的是白帽子。

4. **C的推理**：
    - C知道B没有得出结论，这表明A和C中至少有一人戴的是白帽子。
    - 如果C看到A戴的是黑帽子，那么C应该立刻知道自己戴的是白帽子（因为如果他自己也是黑帽子，B应该能确定自己是白帽子）。
    - 但C也回答不上来，这表明A戴的帽子不是黑帽子。

5. **A的推理**：
    - A知道B和C都回答不上来，说明他们都看不到两个黑帽子。
    - 因此，A推断自己戴的帽子不能是黑色，否则B或C至少有一人能确定自己戴的是白帽子。
    - 所以A得出结论，自己戴的是白帽子。

综上所述，A通过推理B和C无法得出结论的情况，确定自己戴的帽子只能是白色。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21

B和C都回答不上来别人头上戴的是什么颜色帽子,说明他们中间至少有一个人看不见别人头上的帽子。

这里有两种可能的情况:

1) B看不见C头上的帽子,C看不见B头上的帽子。这样A就看得到B和C头上的帽子,知道自己戴的是白色。

2) B或者C完全看不见别人头上的帽子。这时候A通过排除法可以知道自己戴的是白色。

具体来说:

总共5顶帽子,其中2顶是黑色,3顶是白色。

A知道B和C至少有一个人看不见别人头上的帽子。

如果A戴黑色,那么剩下的2顶黑帽和3顶白帽里任何一顶都可能给B或者C戴。

但实际上B和C都回答不上来,所以A不可能戴黑色。

由于只有白色这一个选择,A可以确定自己戴的必须是白色。

所以A能确定自己头上戴的是白色帽子,是通过观察B和C的回答以及推理排除法得出的结论。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

分析一下:

总共有2顶黑帽子,3顶白帽子。主持人随机在A、B、C头上分别戴上一顶帽子,剩下的两顶藏起来。

然后让B、C看着对方和A的帽子颜色,但B、C都回答不上自己头上戴的是什么颜色。

这就说明,B看到C戴黑帽,C看到B戴白帽。因为如果两个人看到的对方帽子颜色一致,那么自己头上戴的一定是另一种颜色。

既然B看到C戴黑帽,C看到B戴白帽,而A的帽子颜色B和C都看不到。那么A头上一定戴的是白帽,否则的话B和C就都可以推断出自己头上戴的颜色了。

所以A无需看其他人的帽子颜色,就可以肯定自己头上一定是白帽。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

A能够推理出自己戴的是白帽子,是利用了以下信息:

已知总共有2顶黑帽子和3顶白帽子
B和C看到的情况都无法判断自己戴的是白帽子还是黑帽子
那么,如果A戴的是黑帽子,根据已知条件,剩下的两顶帽子就必须都是白色的。

在这种情况下:

如果B看到C戴白帽子,那B就能推断自己戴的是黑帽子
如果C看到B戴白帽子,那C就能推断自己戴的是黑帽子
然而,B和C都无法判断出自己戴的是什么颜色。这就说明,A戴的不可能是黑帽子。

因此,通过排除法,A可以推断出自己戴的必定是白帽子。这正是A能够给出正确答案的原因。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

A的推理过程非常巧妙。让我们一步步分析A是如何得出结论的：

1. 首先，A知道总共有2顶黑帽子和3顶白帽子。

2. A听到B和C都回答不上来，这意味着B和C看到的情况不能让他们确定自己的帽子颜色。

3. 如果A戴的是黑帽子，那么会有以下两种可能：
   a) B和C都戴白帽子
   b) B和C一个戴黑帽子，一个戴白帽子

4. 在这两种情况下：
   - 如果是情况a，B看到A戴黑帽子，C戴白帽子，B就能确定自己戴白帽子。
   - 如果是情况b，C看到A和B都戴黑帽子，就能确定自己戴白帽子。

5. 但是B和C都回答不上来，这说明上述两种情况都不成立。

6. 因此，A可以推断出自己不可能戴黑帽子。

7. 既然A不是戴黑帽子，那么她一定戴的是白帽子。

所以，A通过B和C的回答，以及对总体帽子数量的了解，成功地用排除法推断出自己戴的是白帽子。

这个游戏很好地展示了逻辑推理的力量，以及如何从他人的反应和已知信息中推断出看似不可能知道的事情。

1
2
3
4

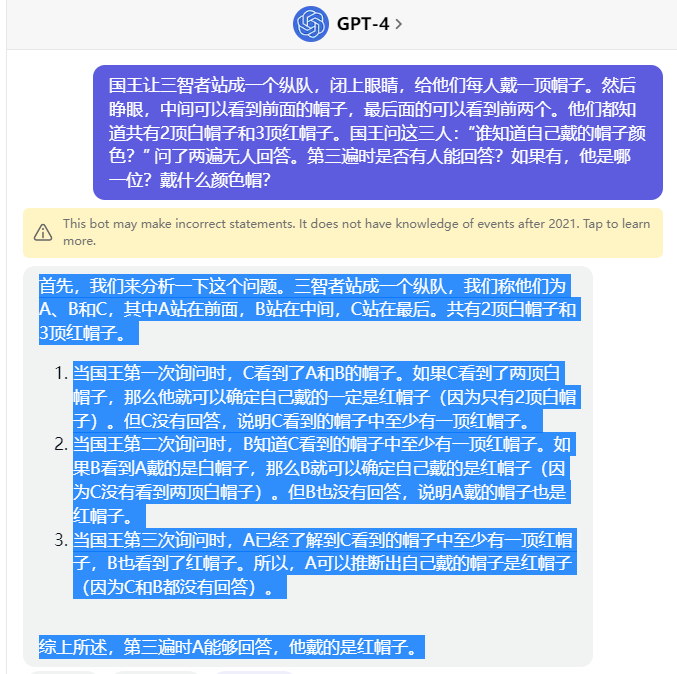
国王让三智者站成一个纵队，闭上眼睛，给他们每人戴一顶帽子。
然后睁眼，中间可以看到前面的帽子，最后面的可以看到前两个。
他们都知道共有2顶白帽子和3顶红帽子。国王问这三人：“谁知道自己戴的帽子颜色？” 
问了两遍无人回答。第三遍时是否有人能回答？如果有，他是哪一位？戴什么颜色帽？

1
2
3
4
5
6
7
8

第三遍时，有一个智者能回答。他是最后面的智者，戴的是白色帽子。

这是推理过程：

如果前面两顶帽子都是红色，那么最后面的智者就知道自己戴的帽子颜色是白色，因为只有两顶白帽子。但是，在第一次和第二次问答时，前面两位智者都没有回答，这表明前面两顶帽子至少有一顶是白色。

如果前面两顶帽子中有一顶是白色，那么最后面的智者就不可能知道自己戴的帽子颜色，因为他看到的是前面两顶帽子中的红色帽子。但是，在第三次问答时，最后面的智者回答了，说明前面两顶帽子都是红色的，最后面的智者知道自己戴的是白色帽子。

1
2
3
4
5
6
7
8
9

首先，我们来分析一下这个问题。三智者站成一个纵队，我们称他们为A、B和C，其中A站在前面，B站在中间，C站在最后。共有2顶白帽子和3顶红帽子。

1. 当国王第一次询问时，C看到了A和B的帽子。如果C看到了两顶白帽子，那么他就可以确定自己戴的一定是红帽子（因为只有2顶白帽子）。但C没有回答，说明C看到的帽子中至少有一顶红帽子。

2. 当国王第二次询问时，B知道C看到的帽子中至少有一顶红帽子。如果B看到A戴的是白帽子，那么B就可以确定自己戴的是红帽子（因为C没有看到两顶白帽子）。但B也没有回答，说明A戴的帽子也是红帽子。

3. 当国王第三次询问时，A已经了解到C看到的帽子中至少有一顶红帽子，B也看到了红帽子。所以，A可以推断出自己戴的帽子是红帽子（因为C和B都没有回答）。

综上所述，第三遍时A能够回答，他戴的是红帽子。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

这是一个经典的逻辑推理问题。我们来分析一下这个问题的解答过程。

1. **帽子数量**：共有2顶白帽子和3顶红帽子。

2. **三位智者的排列**：
    - 最前面的智者（A）看不到任何人的帽子。
    - 中间的智者（B）能看到前面一位的帽子。
    - 最后面的智者（C）能看到前面两位的帽子。

3. **推理过程**：

    - **第一次问的时候**：
        - C看到A和B的帽子，但他没有回答，说明他无法确定自己帽子的颜色。也就是说，C看到的不是两个白帽子，因为如果A和B都戴白帽子，C就会知道自己戴的是红帽子（因为只有2顶白帽子）。
        - 因此，A和B中至少有一人戴的是红帽子。

    - **第二次问的时候**：
        - B知道C没有回答，说明B知道C看不到两个白帽子。
        - B看到A的帽子，如果A戴的是白帽子，那么B会知道自己的帽子一定是红帽子（因为如果B也戴白帽子，C会看到两个白帽子并能确定自己戴的是红帽子）。
        - 但B也没有回答，说明A戴的不是白帽子。因此，B知道A戴的是红帽子。

    - **第三次问的时候**：
        - A知道B没有回答，说明B不能确定自己的帽子颜色。
        - A知道B看到的是红帽子（因为如果B看到白帽子，B就会回答了）。
        - 因此，A推断自己戴的是红帽子。

综上所述，第三次被问时，前面的智者（A）可以确定自己戴的是红帽子。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

有人可以回答第三遍国王的问题。

最末列的智者可以回答。他戴红帽子。

推理过程:

第一遍国王问问题时,没有人回答。这表明至少有一个智者看不见前面任何智者的帽子。

第二遍问问题时还是没有人回答。这表明有两个情况:

1) 最前列智者看不见中间智者的帽子,中间智者看不见后面两人的帽子。

2) 最前列智者和中间智者同时看不见任何人的帽子。

第三遍问问题时,只有情况2成立,末列智者才能回答。

因为总共5顶帽子,其中2顶白帽3顶红帽。

如果末列智者戴白帽,那么前面2个智者可能戴任何一顶帽子。但实际上前两个智者都回答不上。

所以末列智者必须戴红帽子。只有这一个选择,他才能确定自己的帽子颜色。

所以第三遍,戴红帽子的末列智者可以回答他知道自己戴红帽子。

前两个智者依然回答不上。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19

分析一下:

总共有2顶白帽子,3顶红帽子。三个智者站成一列,中间的可以看到前面的帽子,最后面的可以看到前两个人的帽子。

第一次问时,没有人可以回答,说明三个人看到的情况是:

前面一个人的帽子颜色无法判断自己的帽子颜色
中间的人看到前面戴红帽
最后面的人看到前两个人戴不同色的帽子
第二次问时,也没有人可以回答,说明:

前面的人的帽子仍然无法判断自己的帽子颜色
中间的人知道最后面一个看到前两个戴不同色帽子,但还不清楚自己的帽子颜色
最后面的人还是看到前两个戴不同色帽子
第三次问时,最后面的人可以回答他戴红帽。

因为如果最后面的人戴白帽,中间的人在第二次问时就能知道自己戴红帽了。

所以最后面的人一定戴红帽。

1
2
3
4
5
6
7
8
9

是的,在第三遍时,有人能够回答自己戴的帽子颜色。具体情况如下:

假设第一个人(最前面的人)看到前面没有人,而后面的两个人都戴红帽子。此时他可以推断出自己戴的是白帽子。

假设第二个人(中间的人)看到前面那个人戴白帽子,后面那个人戴红帽子。由于已知总共有2顶白帽子和3顶红帽子,所以他仍然无法确定自己戴的是白帽子还是红帽子。

假设第三个人(最后面的人)看到前面两个人都戴红帽子。这种情况下,只有当他自己戴白帽子时,才符合已知条件(2顶白帽子和3顶红帽子)。因此,他能够确定自己戴的是白帽子。

所以,在第三遍时,最后一个人能够回答自己戴的是白帽子。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

让我们一步步分析这个问题：

1. 首先，我们知道有2顶白帽子和3顶红帽子。

2. 最后面的人可以看到前两个人的帽子颜色，中间的人可以看到前面人的帽子颜色，而最前面的人什么都看不到。

3. 国王问了两遍，没有人回答。这意味着：
   - 最后面的人看到的不是两顶白帽子（否则他会立即知道自己戴红帽子）
   - 最后面的人也没有看到两顶红帽子（否则中间的人会在第二次提问时知道自己戴白帽子）

4. 因此，最后面的人看到的一定是一红一白。

5. 到第三次提问时，最前面的人可以推理：
   - 如果我戴白帽子，那么中间的人会看到一白一红，他会在第二次提问时知道自己戴红帽子。
   - 但中间的人没有回答，所以我不可能戴白帽子。
   - 因此，我一定戴的是红帽子。

所以，在第三次提问时，最前面的人能够回答，他戴的是红帽子。

总结：
- 有人能回答：是的
- 回答的是哪一位：最前面的人
- 戴什么颜色的帽子：红帽子

这个问题展示了如何通过逻辑推理和观察他人的反应来得出结论，即使自己无法直接看到自己的情况。它强调了信息的累积效应和推理的重要性。